
CSTR Reactors : mass balance expression
Follow us on Twitter ![]()
Question, remark ? Contact us at contact@myengineeringtools.com
1. CSTR reactor
2. CSTR reactor perfectly stirred and in steady state : mass balance
3. CSTR reactor perfectly stirred and in steady state : reaction speed
CSTR reactors (Continuous Stirred Tank Reactor) are a very widespread class of reactors in chemical or bio chemical industries. The reactor has an inlet, an outlet and is perfectly agitated. This page focusing in applying the general mass balance equations to CSTR reactors.
1. CSTR reactor
A Continuous Stirred Tank Reactor is equipped with an inlet of reactant and an outlet of the content of the reactor which are done continuously during the operation of the reactor.
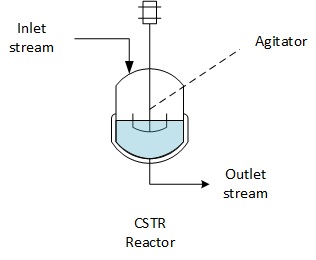
The reactor is equipped with an agitator which is assumed to stir efficiently the reaction medium.
The general mass balance equation can then be expressed the following way :
Inlet = Outlet + Consumption + Accumulation
The units of each component of the expression is a material flowrate : mol/s for instance.
In the applications below, we consider the case that the CSTR reactor considered is :- Perfectly stirred : same concentration at any point in the
reactor's reactive medium
- Isotherm
2. CSTR reactor perfectly stirred and in steady state : mass
balance
Let's assume that reactants A and B are introduced in the reactor.
The reaction
A + B = C +D
is producing C and D. There is only A and B in the inlet, but in the
outlet stream we can find A and B not reacted, and C and D.
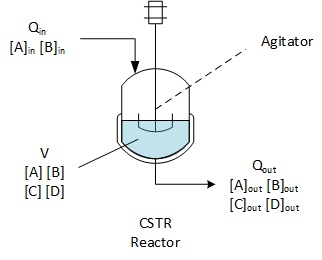
Contrary to Batch and SemiBatch reactors which have a concentration always changing as long as a reaction is happening, CSTR reactors have the properties to be operated in Steady State, which means that a balance is found in between inlet and outlet which allows to prevent accumulation (positive or negative) in the reactor.
Steady state means : dnA/dt = dnB/dt = dnC/dt = dnD / dt = 0
As well as the reactor is in steady state the volume of reaction is not varying over time, which means that we can use directly the volume V in the material balance equation.
The fact to have the reactor is perfectly stirred also helps in expressing the consumption / production of reactants and products as it can be expressed as the product of the reaction speed by the volume (r'V) and concentrations.
Perfectly stirred means :
[A]reactor = [A]out
[B]reactor = [B]out
[C]reactor = [C]out
[D]reactor = [D]out
Reactive A
Qin*[A]in = Qout*[A]out + r'A.V + 0
Reactive B
Qin*[B]in = Qout*[B]out + r'B.V + 0
Product C
0 = Qout*[C]out + rC.V + 0
Product D
0 = Qout*[D]out + rD.V + 0
3. CSTR reactor perfectly stirred and in steady state :
reaction speed
The system of reaction speed can be expressed the following way from the equations above :
r'A = (Qin.[A]in
- Qout*[A]out)/V
r'B = (Qin.[B]in - Qout*[B]out)/V
rC =Qout*[C]out/V
rD = Qout*[D]out/V
Top 5 Most
Popular
1. Compressor
Power Calculation
2. Pump Power Calculation
3. Pipe Pressure
Drop Calculation
4. Fluid Velocity in pipes
5. Churchill Correlation
(friction factor)
4. Residence time
A residence time can be calculated for a CSTR. It corresponds to the time required so that the equivalent of the volume of the reactor enters the reactor. It is important to understand that the time calculated is giving how long all particles will stay in the reactor as some of particles will enter the reactor and leave immediately (almost 0 residence time) while others will stay a very long time, a more precise analysis would be to calculate the distribution of residence time.
The residence time in a CSTR can be calculated by :
τ = V/Qin
With :
τ = residence time in the CSTR reactor (s)
V = volume of the CSTR reactor (m3)
Qin = inlet volumetric flow at the condition of the reactor (m3/s)
Specific case where Qin = Qout
In this case, the relations above can be simplified :
r'A = (Qin.[A]in
- Qout*[A]out)/V = ([A]in
- [A]out)/τ
r'B = (Qin.[B]in - Qout*[B]out)/V
= ([B]in - [B]out)/τ
rC =Qout*[C]out/V = [C]out/τ
rD = Qout*[D]out/V = [D]out/τ