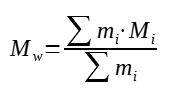---

Polymers : molar mass, number average, mass average calculation, polydispersity

Follow us on Twitter 
Question, remark ? Contact us at contact@myengineeringtools.com

---

1. Number average molar mass
2. Mass average molar mass
3. Polydispersity index
4. Analytical methods to determine a polymer molar mass
5. Impact of molecular mass of polymers

---

Polymers are, as the name indicates, made of several (poly) monomers linked together which can lead to very long chains and very high molar masses. As each polymer in a reactive media has a different length and thus molar mass, how to calculate the molar mass of a particular polymer ?

There are actually several ways to calculate a molar mass depending on what we give priority to.

1. Number average molar mass

The first method is to count the number of polymers having a given mass, then average over the total count of the polymer chains, this gives the number average molar mass M_n

Polymer number average molar mass calculation formula :

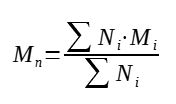
With :

M_n = number average molar mass (g/mol)
N_i = number of polymers having the mass M_i (-)
M_i = molar mass i (g/mol)

The number average molar mass is heavily influenced by small molar masses that are likely to be in larger numbers.

2. Mass average molar mass

Instead of averaging on the number of chains of mass M_i, the average can be on the mass of the polymer chains of mass M_i

Polymer mass average molar mass calculation formula :

With : M_w = mass average molar mass (g/mol)
m_i = mass of the polymer chain of molar mass Mi (-)
M_i = molar mass i (g/mol)

As the mass of long chains is much higher than the one of long chains, the mass average molar mass will give an advantage to long chains, thus :

M_w > M_n

This can be illustrated in the following typical molar mass distribution graph :

3. Polydispersity index

The polydispersity index is the ratio in between the mass average molar mass and the number average molar mass. It will measure the spread in between both averages and will thus give an indication on how wide is the distribution of molar mass for a given polymer.

Polymer polydispersity index formula :

I = M_w / M_n

As we know that Mw > Mn, then I > 1

Typical values of the polydispersity index are :

Polydispersity index	Type of polymerization
I > 1.5	Radical polymerization
I <= 2	Step polymerization

4. Analytical methods to determine a polymer molar mass

In an industrial setting, engineers routinely employ several sophisticated techniques to measure or calculate the molar mass of polymers, each offering unique insights into the polymer's characteristics. Gel Permeation Chromatography (GPC), also known as Size Exclusion Chromatography (SEC), is one of the most widely used methods. GPC separates polymer molecules based on their size, allowing for the determination of both the number average and weight average molar masses. This technique is particularly valuable as it provides a complete distribution of molar masses within a sample, which is crucial for understanding the polydispersity and overall behavior of the polymer. Another common method is viscometry, which measures the viscosity of a polymer solution to estimate its molar mass. Although less detailed than GPC, viscometry is a cost-effective and quick method for obtaining useful data on polymer size.

Engineers leverage these molar mass calculations to predict how polymers will behave under various conditions, such as changes in temperature or mechanical stress. For instance, knowing the molar mass distribution helps in anticipating the mechanical properties of a polymer, such as tensile strength and elasticity. Higher molar mass polymers generally exhibit greater strength and toughness, making them suitable for demanding applications. Conversely, lower molar mass polymers might be used where flexibility and easier processing are required. Additionally, understanding the molar mass can aid in predicting thermal properties, such as the glass transition temperature, which is critical for applications involving temperature variations.

5. Impact of molecular mass of polymers

The molar mass of a polymer significantly influences its physical properties, which in turn dictate its suitability for various applications. For instance, tensile strength and elasticity are directly affected by the molar mass. Generally, polymers with higher molar masses exhibit greater tensile strength due to increased chain entanglements, which enhance the material's resistance to deformation. This makes high molar mass polymers ideal for applications requiring durability and strength, such as structural components in automotive or aerospace industries. Conversely, lower molar mass polymers tend to be less strong but more flexible and easier to process, making them suitable for applications like packaging films or adhesives.

Elasticity, or the ability of a polymer to stretch and return to its original shape, is also influenced by molar mass. Higher molar mass polymers typically show improved elasticity due to the increased length and entanglement of polymer chains, which can more effectively absorb and distribute applied stresses. This property is crucial in applications such as elastic fibers and flexible seals.

Viscosity, another critical property, is highly dependent on molar mass, particularly in the molten state. Higher molar mass polymers generally have higher melt viscosities, which can complicate processing techniques like extrusion or injection molding. These processes require the polymer to flow easily into molds or through dies, and high viscosity can lead to increased energy consumption and processing difficulties. However, a higher melt viscosity can also be beneficial in maintaining the structural integrity of the final product during cooling and solidification.
Variations in molar mass distribution can further influence processing conditions. A narrow molar mass distribution typically results in more uniform processing behavior, as the polymer chains are more consistent in length. This can lead to more predictable flow characteristics and mechanical properties in the final product. In contrast, a broad molar mass distribution can offer a balance between processability and mechanical performance, as the presence of shorter chains can improve flow while longer chains contribute to strength and toughness.

In extrusion and injection molding, understanding and controlling the molar mass distribution is essential for optimizing processing parameters such as temperature, pressure, and shear rate. For example, polymers with a broad distribution might require careful adjustment of processing temperatures to ensure that both high and low molar mass components are adequately melted and mixed. This balance is crucial for achieving the desired properties in the final product while maintaining efficient and cost-effective production processes. By carefully tailoring the molar mass and its distribution, engineers can optimize polymer materials for specific applications, enhancing performance and processing efficiency.

Typical molar mass ranges for different polymer applications and materials:

Application	Typical Molar Mass Range (g/mol)
Plastic bags and bottles	100,000 – 250,000
Tough electronic components	50,000 – 300,000
Structural components for transit applications	50,000 – 300,000
Automotive sector (interior textiles)	10,000 – 50,000
Biomedical materials	3,000,000 – 6,000,000
Flexible seals and elastic fibers	Higher molar mass (varies, generally high)
Non-woven fabrics	10,000 – 50,000
Severe operating conditions (e.g., UHMWPE)	2,000,000 – 6,000,000
High-strength engineering polymer	100,000 – 250,000
Packaging materials	10,000 – 50,000

Polymer Material	Typical Molar Mass Range (g/mol)
High-Density Polyethylene (HDPE)	100,000 – 250,000
Polycarbonate (PC)	50,000 – 300,000
Polyamide (Nylon 6)	10,000 – 50,000
Polyurethane (PU)	50,000 – 300,000
Ultra-High Molecular Weight Polyethylene (UHMWPE)	2,000,000 – 6,000,000
Polystyrene and Polycarbonate (for solubility in organic media)	Varies, typically high
Polyetherols and Polyesterols	Higher molar mass
Polybutadiene (for automotive applications)	Varies based on application

---