
Sound velocity definition and calculation for an ideal gas
Follow us on Twitter ![]()
Question, remark ? Contact us at contact@myengineeringtools.com
| Section summary |
|---|
| 1. Definition of the
sound velocity |
| 2. How to calculate
the sound velocity |
| 3. References of
speed of sound in air |
| 4. Excel calculation tool for sound
velocity |
1. Definition of the sound velocity in an ideal gas
The sound velocity, sometimes also called the speed of sound, is
the distance traveled by a sound wave in a gas during a unit of
time. It is generally expressed in m/s and is used in many process
engineering calculations.
2. How to calculate the sound velocity for an ideal gas
The following formula can be used to calculate the speed of sound in an ideal gas : a = √(k*(R/M)*T)
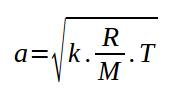
With :
a = speed of sound in m/s
k = specific
heat ratio or isentropic coefficient
R = perfect gas constant = 8314
T = gas temperature in K
M = molecular
weight in g/mol
Top 5 Most
Popular
1. Compressor
Power Calculation
2. Pump Power Calculation
3. Pipe Pressure
Drop Calculation
4. Fluid Velocity in pipes
5. Churchill Correlation
(friction factor)
3. References of speed of sound for common fluids
| Gas |
Speed of sound in m/s |
| Air 20c | 343 m/s |
| Air 100c | 386 m/s |
| Air 150c | 410 m/s |
4. Excel Calculation Tool
The following Excel calculation tool will allow you to calculate the sound velocity for ideal gas : link to Excel calculation tool
Warning : this calculator is provided to illustrate the concepts mentioned in this webpage, it is not intended for detail design. It is not a commercial product, no guarantee is given on the results. Please consult a reputable designer for all detail design you may need.

Sound Velocity Calculator
Sound velocity in ideal gases
Calculation Results
Formula Used:
a = √(k × R × T / M)
Where R = 8.314 J/(mol·K)
Definition of Sound Velocity
The sound velocity (speed of sound) is the distance traveled by a sound wave in a gas during a unit of time. It represents the velocity of small pressure disturbances propagating through the medium and is fundamental in compressible flow analysis.
Theoretical Background
For an ideal gas, the sound velocity is derived from the isentropic process assumption and is given by:
a = √(k × R × T / M)
Where:
- a = speed of sound (m/s)
- k = specific heat ratio (Cp/Cv), dimensionless
- R = universal gas constant = 8.314 J/(mol·K)
- T = absolute temperature (K)
- M = molecular weight (g/mol)
Engineering Applications
Sound velocity is crucial in:
- Compressible flow calculations (Mach number determination)
- Sonic nozzle design and analysis
- Acoustic wave propagation studies
- Gas pipeline analysis under high-velocity conditions
- Turbomachinery design (compressors, turbines)
Key Considerations
This formula applies to ideal gases under the following conditions:
- Low pressure disturbances (linear acoustics)
- Isentropic process assumption
- Ideal gas behavior (PV = nRT)
- Homogeneous gas composition
Reference Sound Velocities for Common Gases
| Gas | Temperature | Sound Velocity (m/s) | Sound Velocity (ft/s) | Molecular Weight (g/mol) | Heat Ratio (k) |
|---|---|---|---|---|---|
| Air | 20°C (68°F) | 343 | 1,125 | 28.97 | 1.40 |
| Air | 100°C (212°F) | 386 | 1,266 | 28.97 | 1.40 |
| Air | 150°C (302°F) | 410 | 1,345 | 28.97 | 1.40 |
| Nitrogen (N₂) | 20°C (68°F) | 349 | 1,145 | 28.01 | 1.40 |
| Oxygen (O₂) | 20°C (68°F) | 326 | 1,070 | 32.00 | 1.40 |
| Carbon Dioxide (CO₂) | 20°C (68°F) | 267 | 876 | 44.01 | 1.30 |
| Methane (CH₄) | 20°C (68°F) | 446 | 1,463 | 16.04 | 1.32 |
| Hydrogen (H₂) | 20°C (68°F) | 1,320 | 4,331 | 2.02 | 1.41 |
| Helium (He) | 20°C (68°F) | 1,007 | 3,304 | 4.00 | 1.67 |
| Argon (Ar) | 20°C (68°F) | 323 | 1,060 | 39.95 | 1.67 |
FAQ: Sound Velocity in Ideal Gases
1. What is sound velocity in an ideal gas?
Sound velocity (or speed of sound) is the distance a sound wave travels in a gas per unit of time, typically measured in meters per second (m/s).
2. How is sound velocity calculated for an ideal gas?
The speed of sound (\( a \)) in an ideal gas is calculated using: \[ a = \sqrt{k \times \frac{R}{M} \times T} \] Where: - \( a \) = Speed of sound (m/s) - \( k \) = Specific heat ratio (isentropic coefficient) - \( R \) = Universal gas constant (8.314 J/(mol·K)) - \( T \) = Gas temperature (K) - \( M \) = Molecular weight (g/mol).
3. What are typical sound velocities in air at different temperatures?
Typical values are: - Air at 20°C: 343 m/s - Air at 100°C: 386 m/s - Air at 150°C: 410 m/s.
4. What is the specific heat ratio (\( k \)) for air?
For air, the specific heat ratio (\( k \)) is approximately 1.4.
5. What is the molecular weight (\( M \)) of air?
The molecular weight of air is approximately 28.97 g/mol.
6. How does temperature affect the speed of sound in a gas?
The speed of sound increases with temperature, as shown in the formula \( a = \sqrt{k \times \frac{R}{M} \times T} \).
7. Are there tools available to calculate sound velocity?
Yes, our website offers a free Excel calculator and an online tool to compute sound velocity in ideal gases.
8. What precautions should be taken when using the calculator?
The calculator is for illustrative purposes only. For detailed design, consult a reputable engineer or designer.
9. Why is sound velocity important in process engineering?
Sound velocity is used in various calculations, such as determining fluid flow rates, pressure drops, and system response times in process engineering.
10. Can the formula be used for gases other than air?
Yes, the formula applies to any ideal gas, provided the correct values for \( k \), \( M \), and \( T \) are used.
Engineering Notes:
Sound velocity is fundamental in compressible flow calculations, acoustic analysis, and Mach number determination.